The Three Pole Trick

We have been authoritatively assured that the curvature
of water can be proved by three poles, and a notable incident
is referred to on the Bedford Canal, Cambridgeshire.
“If three poles of exactly the same height be placed in a line, the
middle one always appears higher than the other two outer ones.
If a telescope be sighted along the first to the third pole, the
top of the middle pole will appear above the line joining the tops of
the two outer ones.” (Italics mine.) Elem. Phys., by R. A. Gregory,
F.R.A.S.

The above paragraph is vague and specious. What is
meant by sighting the telescope “ along ” the first pole to
the third ? Is it. here the trick conies in ? The third pole,
being farthest off, will appear perspectively smaller ; and
the first will not be seen at all if the glass be laid “ along ”
the top of it. The telescope should be placed at some
distance away from the firs pole, when the line of sight
would be found running along the level tops of each pole.
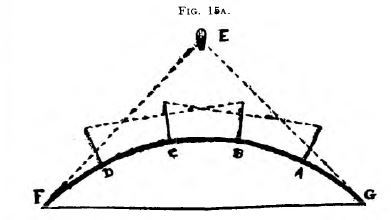
Refer to figures 14 and 15. ‘ The line of sight from A to C
is not parallel to a line tangential at A ; but it ought to be
if there be no trick of collimation in the telescope.
But suppose pole B seems higher than C. Shift the glass
“ along ” B, and add a fourth pole at D, equally high and
distant. Now pole C “ will always ” appear higher than
pole B ; so that C is both lower and higher than B ! Which
is absurd, as Eculid says. Q.E.D.

When the noted wager was tried on the Bedford Canal,
the lens should have been turned half-way round to test
whether there was any “ trick ” in the telescope; but
J. Hampden was not sufficiently sharp. Sir A. R. Wallace
was doubtless honest, but the glass may have tricked him 1
Through a friend I sent him a challenge to shew in print
HOW the bet was won, promising to reply courteously ;
but to me he never replied. Hence of that incident we may
write R.I.P. But I retain copies of the official photographs
taken at the time, in case any other globite cares to pick up
my glove.

My friend “ Parallax ” (Dr. Rowbottam) had tried many
experiments on that canal between 1838 and 1862; and
after the bet affair he again went and carefully tested the
water for six miles, with various powerful telescopes. He
found the surface perfectly level, as before; and his
experiments have several times been pubhshed, but never
refuted. Yet, the canal is still there!
For proof “How they cook science,” see the London
Daily Chronicle, Jan. 14th, 1893.

The above figure 15 illustrates the supposed curvature
when, as is often the case in clear weather, a great extent
of sea surface is visible looking in opposite directions, say
25 miles each way. This should give a dip of 420 feet on
each side. If the sea were globular, the curvature of its
surface ought to be plainly visible, especially from a balloon,
for a sweep of 50 miles, looking both ways; but no such
curvature has ever been seen, even for longer stretches,
but only one vast and uniform level, rising perspectively to
the eye-line. See figure 15b, and compare it with any good
sea-scape. Fig. 15a shews what ought to be seen from a
balloon (E) if the sea were globular.